Advancing Microstrip Patch Antennas through
Prosopis Africana Conductive Ink-Based Thick Films for Enhanced Bandwidth in Radar Applications
Suleiman Babani
,
Mohd Nizar Hamidon
,
Alyani Ismail
,
Haslina Binti Jaafar
,
Intan Helina Hassan
,
Jun-Jiat Tiang
,
Surajo Muhammad
and
Ibrahim Garba Shitu
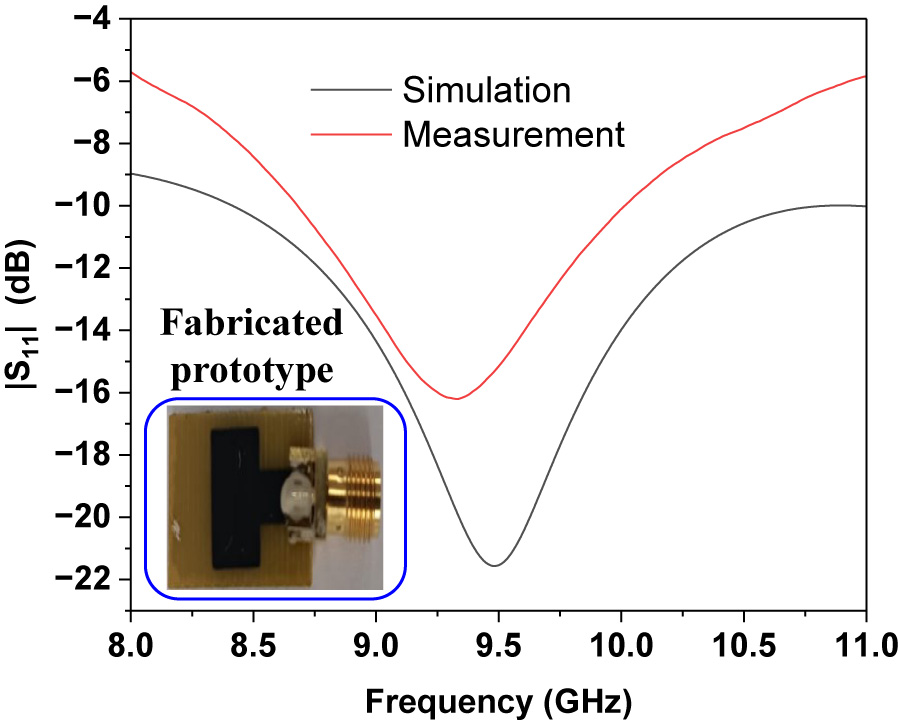
This paper addresses the bandwidth limitations inherent in microstrip patch antennas, which are commonly employed in radar applications owing to their compact size and integration convenience. To overcome these limitations, this study explores the application of Prosopis Africana conductive ink-based thick film, an innovative and environmentally friendly material. Originating from the African mesquite tree, this ink exhibits high conductivity owing to its elevated carbon content, presenting a compelling solution for enhancing microstrip patch antenna bandwidth. The research entails thoroughly examining microstrip antenna design principles and associated challenges, followed by exploring the unique properties of Prosopis Africana conductive ink. A detailed methodology outlines the fabrication process of the ink-based thick layer or film on the substrate, with simulation and measurements employed to evaluate its impact on impedance matching and radiation characteristics. Emphasizing the eco-friendliness of Prosopis Africana conductive ink aligning with green electronics trends, the study showcases its potential for advancing wireless communication systems while reducing ecological footprints. Results demonstrate a substantial bandwidth improvement exceeding 1.85 GHz, a simulation |S11| return loss value of -16.19 dB, and achieved 84.5% radiation efficiency of the operating frequency at 9.5 GHz and a peak realized gain of 7.10 dB. Hence, integrating Prosopis Africana conductive ink-based thick film is a viable strategy for augmenting microstrip patch antenna bandwidth, rendering them more adept for radar applications.