PIER M | PIER Journals

2026-02-16 Latest Published

Anisotropic Modeling of the Electromagnetic Response of 3D-Printed Carbon Nanotube/Polymer Nanocomposites for Shielding Applications
Download Full Article View Full Article

By Ailar Sedghara Ehsan Khoshbakhti Hadi Hosseini Mohammad Arjmand Loïc Markley

Progress In Electromagnetics Research M, Vol. 137, 24-33, 2026

doi:10.2528/PIERM25121402 | Google Scholar

Abstract

This study explores the anisotropic electromagnetic properties of carbon nanotube (CNT)/polylactic acid (PLA) nanocomposites, fabricated in-house and shaped using traditional compression molding and advanced 3D printing techniques. By examining the effects of CNT content (ranging over 1-4 wt.% (weight percent)) and 3D printing path orientation, this research investigates how these factors influence shielding effectiveness (SE) and the corresponding nanocomposite complex dielectric permittivity tensor. Notably, a significant variation in SE was observed between the different printing path orientations, with a difference of over 20 dB at 4 wt.% CNT. Experimental measurements were used to develop an anisotropic model for the complex dielectric permittivity, with the permittivity components for samples at 4 wt.% CNT extracted to be 36.5-j44.5 along the printing direction (ε_||) and 8.3-j3.1 in the perpendicular direction (ε_⊥) over the X-band frequency range (8.2-12.4 GHz). These findings demonstrate that CNT alignment during 3D printing induces highly directional electromagnetic properties. Furthermore, we demonstrate that anisotropic simulation models provide a more accurate prediction of the electromagnetic response of 3D-printed nanocomposite structures than isotropic models. In brief, this study emphasizes the necessity of considering anisotropic properties in the design and simulation of 3D-printed nanocomposites for electromagnetic shielding and other applications.

2026-02-16

PIER M

Vol. 137, 24-33, 2026

doi:10.2528/PIERM25121402

download: 15

Anisotropic Modeling of the Electromagnetic Response of 3D-Printed Carbon Nanotube/Polymer Nanocomposites for Shielding Applications

Ailar Sedghara, Ehsan Khoshbakhti, Hadi Hosseini, Mohammad Arjmand and Loïc Markley

2026-02-06

PIER M

Vol. 137, 13-23, 2026

doi:10.2528/PIERM25111706

download: 109

Design of a Flexible and Tri-Band MIMO Antenna for Conformal Wi-Fi 7/5G Applications

Tian-Xiang Wang, Chengzhu Du and Xi Sun

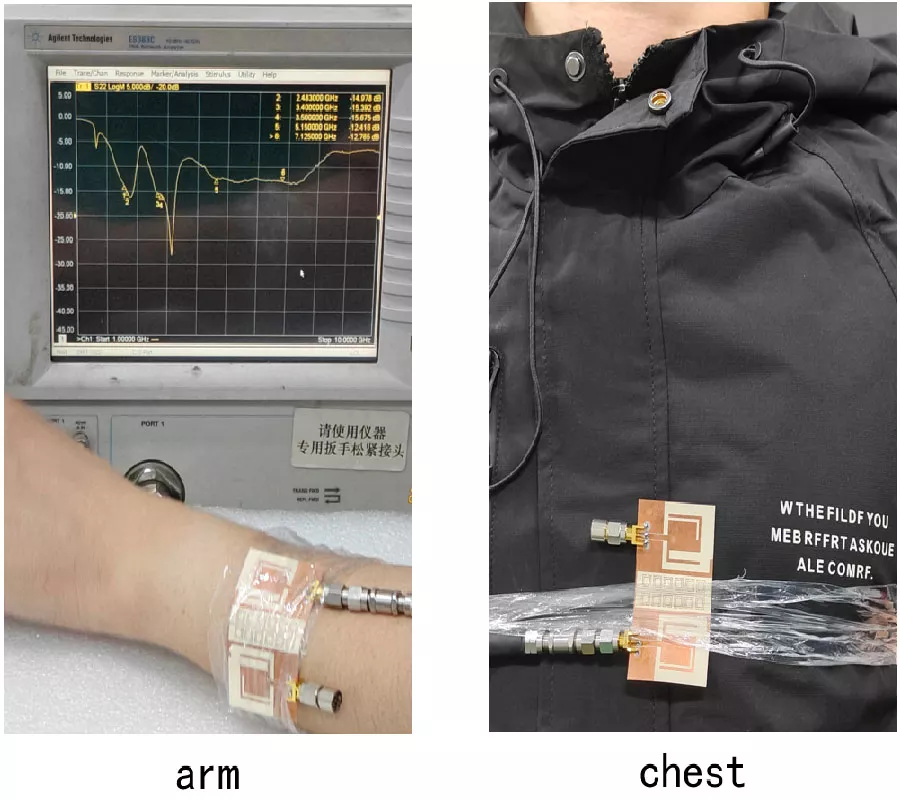
This paper describes a flexible dual-port multiple-input multiple-output (MIMO) antenna system tailored for multi-band operation, covering 2.4 GHz Wi-Fi, 3.5 GHz 5G, as well as the 5-7 GHz band used in wireless applications such as Wi-Fi 7. The antenna is fabricated on a liquid crystal polymer (LCP) substrate, featuring an ultra-thin profile of 0.1 mm and a compact size of 60 × 35 mm², making it highly suitable for integration into modern flexible and wearable devices. To achieve high port isolation, a complementary split-ring resonator (CSRR) structure is incorporated between the two radiating elements. The measurement results indicate that the antenna achieves impedance bandwidths across 1.36-2.71 GHz, 3.07-3.655 GHz, and 4.015-8.245 GHz, which fully cover the target frequency bands of 2.4-2.483 GHz, 3.4-3.5 GHz, and 5.15-7.125 GHz. The antenna's performance is comprehensively characterized by evaluating key parameters including S-parameters, envelope correlation coefficient (ECC), diversity gain (DG), total active reflection coefficient (TARC), gain, mean effective gain (MEG), and radiation patterns, along with other relevant metrics. All measured results confirm that the antenna meets the essential requirements for MIMO and diversity systems. Furthermore, bending tests conducted at two distinct radii of 30 mm and 50 mm confirm stable antenna performance, verifying its mechanical robustness and reliability under practical bending conditions.

Design of a Flexible and Tri-Band MIMO Antenna for Conformal Wi-Fi 7/5G Applications

2026-01-27

PIER M

Vol. 137, 1-12, 2026

doi:10.2528/PIERM25112603

download: 150

A Hybrid Quantum Transport Simulator for MOSFETs Using Non-Equilibrium Green's Function and FDTD

Kai Ren

Based on the time-dependent Schrӧdinger equation, a finite-difference time-domain (FDTD) method is proposed to investigate electron propagation with the presence of tunneling potential distributions in metal-oxide-semiconductor field-effect transistors (MOSFETs). The channel current equation in the drift-diffusion model for classical transport is derived from the probability current formula with a plane wave assumption of the electron's state function. In both classical and quantum regimes, channel currents are numerically simulated based on quantum transport in MOSFETs using transmission functions and Fermi-Dirac distributions. The transmission function is obtained from the non-equilibrium Green's function (NEGF), indicating the probability of electrons through a channel. To determine the number of electrons at both source and drain terminals of a MOSFET, the Fermi-Dirac distributions are calculated. Numerical simulations of channel currents with various external gate-source and drain-source voltages are investigated, showing that a similar peak channel current can be generated with lower external voltages in a smaller MOSFET with a shorter gate length. Electron forward and backward propagations are obtained through FDTD simulations to demonstrate the difference of cutoff modes in classical and quantum MOSFETs.