PIER Letters | PIER Journals

2024-05-14

PIER Letters

Vol. 119, 99-105, 2024

download: 129

Analysis of Fractal AMC Backed Gain Enhancement for Circular Spike Monopole Antenna

Rajesh Katragadda and Palasetti Appala Nageswara Rao

This work provides the design, analysis, and performance optimization of an artificial magnetic conductor (AMC)-based wideband printed monopole antenna. The proposed antenna structure is constituted with CPW feeding, and an AMC layer has been added beneath the proposed antenna configuration to decrease back lobe radiation. By employing an AMC reflector, composed of periodic copper metallic Minkovski square fractal patches on a circular serrated antenna with an air gap separation of 8\,mm, the proposed antenna has obtained a peak gain of 12.9 dBi, and wideband is also achieved by the antenna for wearable applications. The prototyped model of cotton fabric substrate material based measurement results with antenna measurement setup match the CST-tool simulation results, enabling the applicability in real time communication systems.

Analysis of Fractal AMC Backed Gain Enhancement for Circular Spike Monopole Antenna

2024-05-12

PIER Letters

Vol. 119, 91-98, 2024

doi:10.2528/PIERL24032501

download: 133

Cross Polar Reduction of a High Gain Wide-Band Stacked Microstrip Antenna Using Metasurfaces

Anjali Rochkari , Shubhangi Mangesh Verulkar , Nayana Chaskar , Mahadu Annarao Trimukhe and Rajiv Kumar Gupta

In this article, a low-profile high gain stack microstrip antenna (MSA) with low Cross Polarization Level (CPL) using multiple metasurfaces is proposed. MSA on a thick substrate having low dielectric constant enhances the gain and bandwidth (BW). However, as substrate thickness increases, the CPL increases due to increase in coaxial probe length used for feeding MSA. The CPL is reduced by using metasurfaces formed by an array of square metallic patches of dimensions and periodicity < 0.1λ₀. A suspended MSA (SMSA) is designed on a reactive impedance surface (RIS) backed substrate, to reduce the interaction between substrate and ground plane, surface waves and to increase impedance BW and polarization purity. A parasitic patch is fabricated on a superstrate and placed above the SMSA and metallic patches forming the metasurfaces are fabricated around the MSA, PP and on the other side of superstrate. These metasurfaces increase the inductance of the antenna, and to compensate the inductance, the height of SMSA and the spacing between MSA and PP are decreased which results in the decrease in probe feed length and CPL. This novel low-profile high gain wide band stack MSA offers CPL < -20 dB, Side Lobe Level (SLL) < -20 dB, Front to Back lobe ratio (F/B) > 20 dB and S₁₁ ≤ -10 dB over 3.3-3.6 GHz to cover 5G applications. The 0.935λ₀ × 0.99λ₀ × 0.046λ₀ prototype antenna offers peak gain of 8.3 dBi, antenna efficiency >90%, and λ₀ being the free-space wavelength at 3.3 GHz.

Cross Polar Reduction of a High Gain Wide-band Stacked Microstrip Antenna using Metasurfaces

2024-05-05

PIER Letters

Vol. 119, 85-90, 2024

doi:10.2528/PIERL24022103

download: 179

Suppression of Peak Sidelobe Level in Linear Symmetric Antenna Arrays Using Hybrid Grey Wolf and Improved Bat Algorithm

Jiao Zhang , Jiajun Chu , Yufeng Liu and Wenmei Zhang

In this paper, the Hybrid Grey Wolf and Improved Bat Optimization Algorithm (HWIBO) is proposed to reduce the peak sidelobe level (PSLL) of linear symmetric array synthesis with aperture and element spacing constraints. The HWIBO utilizes both the Grey Wolf Optimization (GWO) and Improved Bat algorithms (IBA) simultaneously to optimize PSLL. Each iteration generates two sets of results, and the optimal result is chosen for the next loop. Compared to other algorithms used in simulation of antenna sidelobe suppression, the HWIBO not only inherits the fast convergence advantage of the IBA which enhances population diversity but also possesses the strong global search capability of the GWO. This helps the IBA escape local optima and strengthens the global search capability during the later stages of algorithm iterations. Finally, the simulation results demonstrate the successful reduction of PSLL under various constraints, confirming the effectiveness of the hybrid algorithm.

Suppression of Peak Sidelobe Level in Linear Symmetric Antenna Arrays Using Hybrid Grey Wolf and Improved Bat Algorithm

2024-04-30

PIER Letters

Vol. 119, 79-84, 2024

doi:10.2528/PIERL24032101

download: 201

Underdetermined Equation Model Combined with Improved Krylov Subspace Basis for Solving Electromagnetic Scattering Problems

Cunjie Shen , Xin-Yuan Cao , Qi Qi , Yunuo Fan , Xiangxiang Liu , Xiaojing Kuang , Cheng-Hua Fan and Zhongxiang Zhang

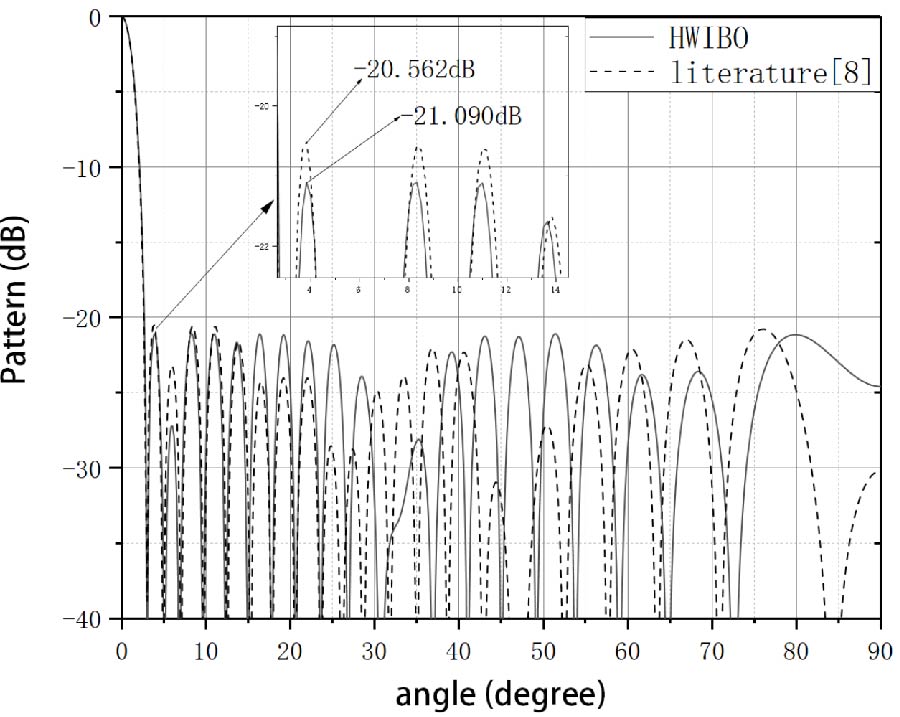
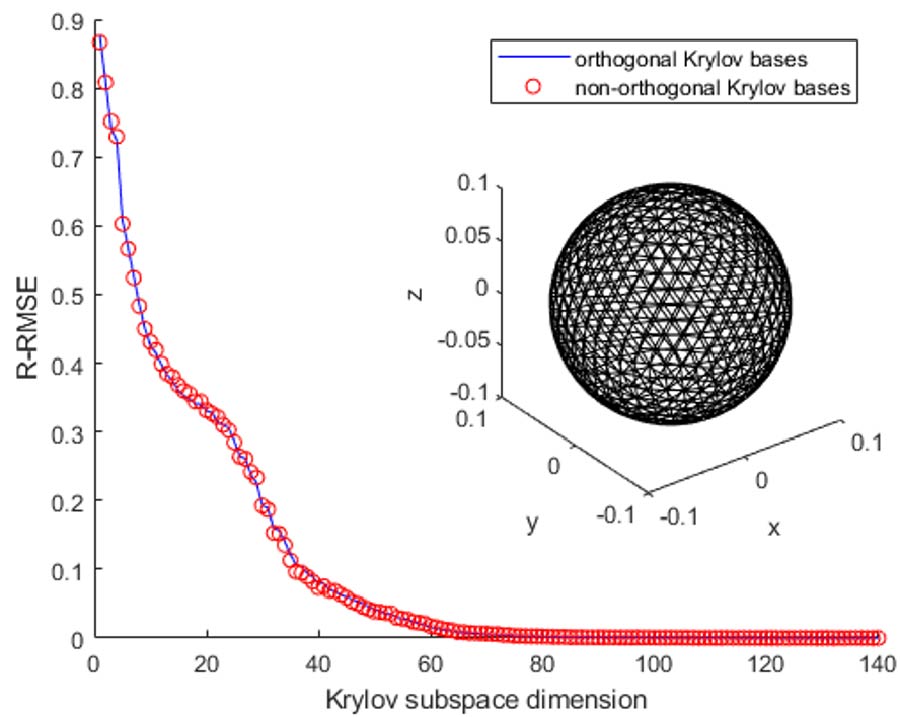
To accelerate the solution of electromagnetic scattering problems, compressive sensing (CS) has been introduced into the method of moments (MoM), Consequently, a computational model based on underdetermined equations has been proposed, which effectively reduces the computational complexity compared with the traditional MoM. However, while solving surface-integral formulations for three-dimensional targets by MoM, due to the severe oscillation of current signals, commonly used sparse bases become inapplicable, which renders the application of the underdetermined equation model quite challenging. To address this issue, this paper puts forward a scheme that employs Krylov subspace, which is constructed with low complexity by meticulously designing a group of non-orthogonal basis vectors, to replace the sparse transforms in the algorithmic framework. The principle of the method is elaborated in detail, and its effectiveness is validated through numerical experiments.

Underdetermined Equation Model Combined with Improved Krylov Subspace Basis for Solving Electromagnetic Scattering Problems

2024-04-25

PIER Letters

Vol. 119, 73-78, 2024

doi:10.2528/PIERL24031001

download: 424

Broadband AMC Metasurface and Its Application for Radar Cross Section Reduction of a Microstrip Antenna

Xutong Wang , Liping Han , Guorui Han , Yufeng Liu and Yanfeng Geng

A broadband artificial magnetic conductor (AMC) metasurface for radar cross section reduction is proposed. Modified Jerusalem cross unit and quasi-circular unit can achieve effective reflection phase difference of 180˚ (±37˚) within a wide frequency range from 8.95-17.3 GHz. The broadband metasurface consists of chessboard-arranged 3 × 3 block arrays, and each block arrays is composed of 4 × 4 AMC units. The proposed AMC metasurface is applied to a microstrip antenna for reducing RCS. The measurement results show that the low RCS antenna can obtain 10 dB RCS reduction from 7.93-17.5 GHz. The relative bandwidth is 75.2%, and the maximum reduction value is 30.2 dB. Also, radiation performance of the antenna is well maintained.

Broadband AMC Metasurface and Its Application for Radar Cross Section Reduction of a Microstrip Antenna

2024-04-23

PIER Letters

Vol. 119, 67-72, 2024

doi:10.2528/PIERL24011401

download: 223

Design of 1.4 GHz WMTS Band Implantable Antenna and Performance Measurement for Bio-Telemetric Applications

Vijayanandam Nithiyanandam and Vidhya Sampath

In this paper, the design and validation of an implantable antenna which is applicable to biotelemetry services is presented. This proposed antenna operates in the wireless medical telemetry service (WMTS) frequency band of 1.39-1.4 GHz. As compared to other contemporary antennas, this design provides better gain of -31 dB and reflection coefficient of -20.2 dB with better safe limit of specific absorption rate (SAR). At the resonating frequency of 1.4 GHz, the intended antenna provides good radiation and gain characteristics. The VSWR parameter for this designed antenna has been obtained as 1.25 which promises for proper impedance match. The designed antenna has been fabricated and validated with tissue mimic liquid-phantom to make sure the suitability for implantation. The simulated measurements have a close agreement with the experimentally measured results.

Design of 1.4 GHz WMTS Band Implantable Antenna and Performance Measurement for Bio-telemetric Applications

2024-04-21

PIER Letters

Vol. 119, 59-65, 2024

doi:10.2528/PIERL24030403

download: 291

A Compact Wideband Waveguide Filtering Antenna with Transmission Zero

Iqram Haider , Ananjan Basu and Shiban Kishen Koul

This letter describes the design of a third-order, compact, wideband waveguide filtering antenna with a transmission zero (TZ) in the upper stopband. A novel frequency-variant coupling (FVC) network that provides a TZ in addition to the pole is used to achieve compactness and higher selectivity. The position of the TZ can be changed in the upper stopband by altering the physical parameters of the proposed FVC. The radiating waveguide aperture is matched to the real admittance of the generator over a wide bandwidth by utilizing coupled-resonator theory. This leads to a wide fractional bandwidth of 23%, along with a TZ at the upper stopband. The filtering antenna has been manufactured using metal 3-D printing to achieve low manufacturing costs and light weight. The measured results are in good agreement with the simulated ones, which shows the feasibility of the proposed FVC structure for the design of the waveguide filtering antenna with a TZ.

A Compact Wideband Waveguide Filtering Antenna with Transmission Zero

2024-04-13

PIER Letters

Vol. 119, 51-57, 2024

doi:10.2528/PIERL24012503

download: 310

Application of Improved SROM Based on RBF Neural Network Model in EMC Worst Case Estimation

Bing Hu , Yingxin Wang , Shenghang Huo and Jinjun Bai

The Stochastic Reduced-Order Models (SROM) is a non-embedded uncertainty analysis method that has the advantages of high computational efficiency, easy implementation, and no dimensional disasters. Recently, it has been widely used in the field of EMC simulation. In the process of optimizing electromagnetic protection design, the worst-case estimation value is an extremely important uncertainty quantification simulation result. However, the SROM has a large error in providing this result, which limits its application in the field of EMC simulation prediction. An improved SROM based on the Radial Basis Function (RBF) neural network algorithm is proposed in this paper, which improves the fitness function in the genetic algorithm center clustering process and constructs an RBF neural network model to obtain accurate worst-case estimation results. The accuracy improvement effect of the algorithm proposed in this paper in worst-case estimation is quantitatively verified by using a parallel cable crosstalk prediction example from published literature.

Application of Improved SROM Based on RBF Neural Network Model in EMC Worst Case Estimation

2024-04-12

PIER Letters

Vol. 119, 43-50, 2024

doi:10.2528/PIERL23112703

download: 258

Frequency Reconfigurable Antenna Design and Analysis with White LED Lamp, Red and Infrared LEDs

Valsalam Reji and Chellappan Thangappan Manimegalai

This research presents a frequency reconfigurable antenna analysis for wireless applications using multiple light sources. The antenna is constructed on a Roger substrate with (44x28) mm² dimensions. The antenna comprises two parallel tuner arrangements in addition to a V-shaped radiating section. Two optical PIN photodiodes are connected to the two parallel monopole tuners, which serve as the antenna's switching component and are utilized to adjust the resonant frequency. These two PIN photodiode switches work in the 600-1050 nm wavelength range. To analyze the antenna performance, four different optical sources are used. They are white colour LED lamp, 650 nm optical fiber, red LEDs, and IR LEDs. In every case, the antenna performance analysis are carried out for all the four logic state of the switches (00, 01, 10, 11). Under white lamp test conditions, the antenna's maximum gain is 6 dBi, and when red LEDs are employed as the optical source, its maximum bandwidth is 21%. The antenna reconfigurable frequencies are 3.5 GHz and 5-5.8 GHz (5, 5.2, 5.5, 5.8 GHz).

Frequency Reconfigurable Antenna Design and Analysis with White LED Lamp, Red and Infrared LEDs

2024-04-11

PIER Letters

Vol. 119, 35-41, 2024

doi:10.2528/PIERL24030104

download: 366

SIW Filter Based on a CPW Resonator and a Hybrid Electromagnetic Coupling Structure

Xiaohei Yan , Minjie Guo , Wenjing Mu , Xiumei Huang and Haiyan Zeng

This paper proposes a hybrid cross-coupled filter that utilizes a coplanar waveguide (CPW) resonator and a hybrid electromagnetic coupling structure. The filter features a flexible and controllable position of the transmission zeros and a quasi-elliptical response. It is composed of two CPW structures etched within the upper metal surface of a second-order substrate-integrated waveguide (SIW) resonant cavity. By adjusting the dimensions of the two CPW structures between the SIW resonant cavities and the width of the inductive coupling window, the strengths of the electric and magnetic couplings can be easily controlled to achieve a controllable hybrid cross-coupling effect in order to adjust the position of the transmission zeros and ultimately to realize the third-order filter with quasi-elliptical response characteristics. Simulation and test results indicate that the filter has a center frequency of 4.55 GHz, a -3 dB bandwidth of 180 MHz, a relative bandwidth of 4%, an insertion loss of -0.9 dB in the passband, a return loss of over 15 dB, and two transmission zeros located at 4.4 GHz and 4.7 GHz, respectively. The filter has several advantages, including a simple structure, low insertion loss, small circuit size, good frequency selectivity, and flexible and controllable transmission zeros. These features make it suitable for use in 5G (sub-6 GHz) wireless communication systems.

SIW Filter Based on a CPW Resonator and a Hybrid Electromagnetic Coupling Structure

2024-04-05

PIER Letters

Vol. 119, 27-33, 2024

doi:10.2528/PIERL24030407

download: 331

A Compact MIMO Antenna with Wideband Charaecteristics for WiFi 6E/X-Band Applications

Janani Sasikumar and Kanmani Ruby Erode Dhanapal

A novel proposal for upcoming wireless applications introduces a dual-band, highly decoupled, and compact microstrip patch co-planar waveguide (CPW)-fed MIMO antenna. This low-profile antenna exhibits narrow wide-band performance across the frequency bands of 6.2 to 11.2 GHz, with dimensions of 20 × 20 mm³ on a standard FR4 substrate. Through integration onto a printed circuit board (PCB) measuring 20 × 20 mm², the antenna configuration is expanded to a 4 × 4 MIMO arrangement. Individual antennas within this setup maintain a significant isolation of around 20 dB in the absence of a decoupling mechanism. Fabrication of the designed four-port antenna allows for practical measurement of various antenna parameters. The measured results closely align with simulated outcomes, encompassing S parameters, far-field patterns, and MIMO characteristics such as envelope correlation coefficient, channel capacity loss, and total active reflection coefficient. These results suggest that the antenna design presented in this study holds promise for future wireless applications.

A Compact MIMO Antenna with Wideband Charaecteristics for WiFi 6E/X-band Applications

2024-04-03

PIER Letters

Vol. 119, 21-26, 2024

doi:10.2528/PIERL24010804

download: 327

Comparative Study of High-Resolution RCS Models of Motorcyclists in W-Band Extracted from Measurements

Sevda Abadpour , Mario Pauli , Jan Siska , Nils Pohl and Thomas Zwick

Reliably modeling vulnerable road users (VRUs) such as motorcyclists in the virtual environment is indispensable in developing over-the-air (OTA) validation test methods. However, there are still challenges arising from many possible variations of VRUs, which may participate in the traffic scenarios. Therefore, it is essential to model them precisely and demonstrate consistency between virtual evaluation and reality. To achieve this goal, the VRUs must be modeled based on their backscattering behavior which can be prepared based on high-resolution (HR) radar cross section (RCS) measurements. This work presents the backscattering behavior of motorcyclists as one of the critical VRUs in traffic scenarios. The extracted model of a motorcyclist is analyzed and compared based on HR-RCS measurements with different motorcycle variants. This evaluation is a prerequisite for developing a realistic model of VRUs and ensuring an adequate level of accuracy.

Comparative Study of High-resolution RCS Models of Motorcyclists in W-band Extracted from Measurements

2024-04-03

PIER Letters

Vol. 119, 15-19, 2024

doi:10.2528/PIERL24021403

download: 340

A Simplified Extended Multilayer SIW Supporting TE₀₁ Mode Integrated with a Feeding Structure

Tzichat M. Empliouk , Christos I. Kolitsidas and George Kyriacou

In this letter, a TE₀₁ operation of a multilayered Substrate Integrated Waveguide (SIW) is presented. To enable the propagation of this typically unsupported mode, the SIW is integrated with feeding layer and with an Electromagnetic Band Gap (EBG) structure, exciting and confining the field within the proposed waveguide structure. The EBG is simply stacked on top and bottom of the proposed structure, allowing for ease of manufacturing. The overall proposed structure is simulated and measured, and the results indicate very low insertion loss in the passband of the waveguide.

A Simplified Extended Multilayer SIW Supporting TE<sub>01</sub> Mode Integrated with a Feeding Structure

2024-03-30

PIER Letters

Vol. 119, 7-13, 2024

doi:10.2528/PIERL24021201

download: 383

A Novel Filter with Reconfigurable Bandwidth OR Transmission Zeros Based on a Multiple-Mode Stub-Loaded Resonator

Liangzu Cao and Shouzhan Li

This paper presents a novel bandpass filter with reconfigurable bandwidth or transmission zeros. The proposed filter is based on a multiple-mode stub-loaded resonator. Three PIN diodes are utilized as switching elements to achieve four switchable operating states. The measurement results indicate that the 3 dB fractional bandwidth (FBW) of the filter can be varied from 32.3% to 70% at the centre frequency of 2.2 GHz, and the stopband attenuation is higher than 35 dB. The filter size is only about 0.28λ_g×0.19λ_g.

A Novel Filter with Reconfigurable Bandwidth or Transmission Zeros Based on a Multiple-mode Stub-loaded Resonator

2024-03-26

PIER Letters

Vol. 119, 1-6, 2024

doi:10.2528/PIERL24020702

download: 453

Scanned Antenna Arrays with Random Deactivated Elements

Noor Waadullah Yaseen and Jafar Ramadhan Mohammed

Usually inactive or also known as thinned elements are used to simplify the array design complexity by turning off some of the active elements in uniformly filled arrays. Consequently, the far-field radiation characteristics such as sidelobe level, beamwidth, and directivity may be negatively changed if no optimizer is used. Further, these radiation characteristics may be unavoidably deteriorated when the main beam is scanned to new directions other than the referenced broadside direction. In this paper, an efficient optimization method based on the genetic algorithm and a dynamic deactivation method is proposed to randomly deactivate a number of array elements to minimize the peak sidelobe level and at the same time maintain the array directivity undistorted, while scanning the main beam. The deactivation method chooses optimally the suitable number of elements and their locations that need to be deactivated such that the resulting radiation characteristics positively change according to the specified cost function. Also, the proposed scanned array uses binary coefficients to activate and deactivate the array elements, thus, the feeding network of the proposed array is very simple, and it can be easily implemented in practice. Through extensive simulation results, we show that the proposed optimization method has good performance under wide range of scanned main beam directions. It is also found that the number of deactivation elements (i.e., the optimization variables) increases with larger scan angle.