2026-01-27 Latest Published
By Kai Ren
Progress In Electromagnetics Research M, Vol. 137, 1-12, 2026
Abstract
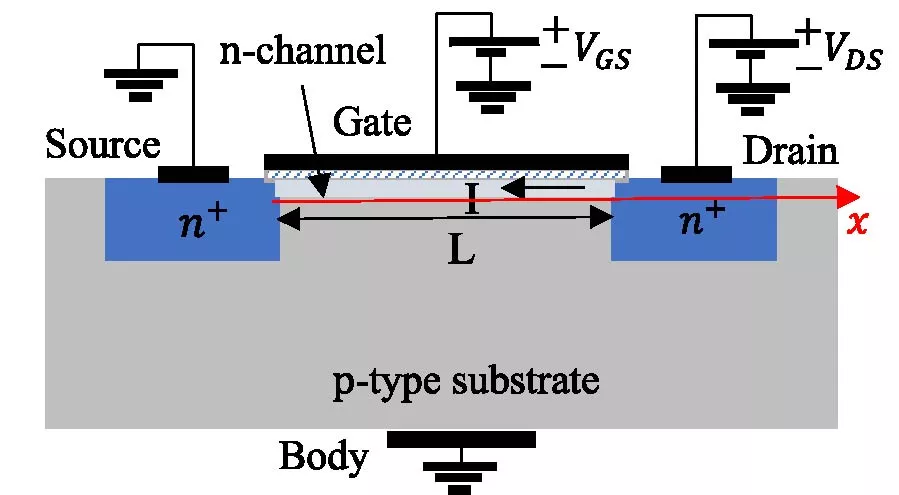
Based on the time-dependent Schrӧdinger equation, a finite-difference time-domain (FDTD) method is proposed to investigate electron propagation with the presence of tunneling potential distributions in metal-oxide-semiconductor field-effect transistors (MOSFETs). The channel current equation in the drift-diffusion model for classical transport is derived from the probability current formula with a plane wave assumption of the electron's state function. In both classical and quantum regimes, channel currents are numerically simulated based on quantum transport in MOSFETs using transmission functions and Fermi-Dirac distributions. The transmission function is obtained from the non-equilibrium Green's function (NEGF), indicating the probability of electrons through a channel. To determine the number of electrons at both source and drain terminals of a MOSFET, the Fermi-Dirac distributions are calculated. Numerical simulations of channel currents with various external gate-source and drain-source voltages are investigated, showing that a similar peak channel current can be generated with lower external voltages in a smaller MOSFET with a shorter gate length. Electron forward and backward propagations are obtained through FDTD simulations to demonstrate the difference of cutoff modes in classical and quantum MOSFETs.