PIER | PIER Journals

2004-04-15

PIER

Vol. 47, 313-333, 2004

doi:10.2528/PIER03120301

download: 224

Reduction of Errors in Antenna Radiation Patterns Using Optimally Truncated Spherical Wave Expansion

Paivi Koivisto

This paper demonstrates how the error of a measured or simulated antenna radiation pattern can be decreased by calculating a spherical wave expansion (SWE) with an optimised truncation mode index. Four radiation pattern examples are examined for which the analytical expression of the electrical field is known. Upon adding random and Î¦-alignment errors to the exact electric fields, the SWEs are determined and compared with the corresponding ones for the exact fields. These comparisons show that the accuracy of the calculated SWE is much better than the accuracy of the original inaccurate field. Resting on the calculated examples, a method is created which can be used to determine the optimal truncation index from the modal power distribution of a SWE without knowing the exact field. Finally, the method developed is applied to measured antenna radiation patterns.

REDUCTION OF ERRORS IN ANTENNA RADIATION PATTERNS USING OPTIMALLY TRUNCATED SPHERICAL WAVE EXPANSION

2004-04-15

PIER

Vol. 47, 297-312, 2004

doi:10.2528/PIER04010201

download: 211

Analysis of a Coaxial Waveguide Corrugated with Wedge-Shaped Radial Vanes Considering Azimuthal Harmonic Effects

Kalpana Singh , Pradip Kumar Jain and B. N Basu

The analysis was developed for a coaxial waveguide for two configurations - one in which the central conductor is corrugated in axial slot-wedges, with ridge-wedges between them, and the other in which the outer conductor is provided with radial metal vane-wedges. Azimuthal harmonics were considered in the structure regions, the effects of which were ignored in earlier published analyses based on the surface impedance model to replace the interface between the two structure regions by a homogeneous reactive surface. For both the structure configurations, one and the same form of the dispersion relation with proper interpretation of the symbol for the radius of the ridge/vane was obtained. The dispersion relation obtained by the present analysis was validated against that obtained by other analytical methods reported in the literature. The shape of the dispersion characteristics is found uncontrollable by the structure parameters, and therefore the structure cannot be used for broadbanding a gyro-TWT. However, the plot of the eigenvalue versus the ratio of the outer conductor to ridge/vane radii strongly depended on the ridge/vane parameters. Thus the structure with its cross section tapered and ridge/groove parameters optimized has the potential for providing mode rarefaction in high-power, over-sized, over-moded gyrotrons.

ANALYSIS OF A COAXIAL WAVEGUIDE CORRUGATED WITH WEDGE-SHAPED RADIAL VANES CONSIDERING AZIMUTHAL HARMONIC EFFECTS

2004-04-15

PIER

Vol. 47, 263-296, 2004

doi:10.2528/PIER03122304

download: 213

Reflection and Transmission from a Thin Inhomogeneous Cylinder in a Rectangular Te10 Waveguide

M. Booty and Gregory A. Kriegsmann

We study the scattering problem for a thin cylindrical target that is placed with arbitrary orientation in a rectangular TE₁₀ waveguide and subjected to an imposed electromagnetic field. The scattered far-field is expressed in terms of the scattered field inside the target and the far-field expansion of the dyadic Green's function for the waveguide. In order to capture features of interest in microwave heating applications, we allow the target material's electrical properties to be arbitrary functions of position along the thin cylindrical target's axis. Reflection and transmission coefficients for such a target, and an expression for the rate of deposition of electromagnetic energy within it are derived.

REFLECTION AND TRANSMISSION FROM A THIN INHOMOGENEOUS CYLINDER IN A RECTANGULAR TE10 WAVEGUIDE

2004-04-15

PIER

Vol. 47, 235-262, 2004

doi:10.2528/PIER03122201

download: 322

Electrostatic Image Theory for an Anisotropic Boundary of an Anisotropic Half-Space

J. Hanninen , Ismo Veikko Lindell and K. Nikoskinen

A novel image solution for the canonical electrostatic problem of a point charge in an anisotropic half-space bounded by an anisotropic surface is presented. The image source is obtained in operator form by using Fourier-transformed Maxwell equations and transmission line theory. After applying methods from Heaviside operator calculus, the image operator can be interpreted as a combination of a point charge and a line-charge-bounded sector of planar charge density. The new theory is shown to coincide with the previously known image solutions of less general anisotropic media. In addition to being applicable to any physically feasible anisotropic medium of electrostatics, the method can be used for steady-current conductivity problems via a duality transformation.

ELECTROSTATIC IMAGE THEORY FOR AN ANISOTROPIC BOUNDARY OF AN ANISOTROPIC HALF-SPACE

2004-04-15

PIER

Vol. 47, 213-234, 2004

doi:10.2528/PIER04020403

download: 201

On Sampling-Biorthogonal Time-Domain Scheme Based on Daubechies Compactly Supported Wavelets

Youri Tretiakov , Stanislav Ogurtsov and George Pan

The multi-resolution time domain (MRTD) technique for electromagnetic field equations was proposed by Krumpholz, Katehi et al., using Battle-Lemarie wavelets. The basis principle behind the MRTD is the wavelet-Galerkin time domain (WGTD) approach. Despite its effectiveness in space discretization, the complexity ofthe MRTD makes it unpopular. Recently, the WGTD was significantly simplified by Cheong et al. based on the approximate sampling property ofthe shifted versions ofthe Daubechies compactly supported wavelets. In this paper, we provide a rigorous analysis ofthe MRTD, employing positive sampling functions and their biorthogonal dual. We call our approach as the sampling biorthogonal time-domain (SBTD) technique. The introduced sampling and dual functions are both originated from Daubechies scaling functions of order 2 (referred as to D₂), and form a biorthonormal system. This biorthonormal system has exact interpolation properties and demonstrates superiority over the FDTD in terms ofmemory and speed. Numerical examples and comparisons with the traditional FDTD results are provided.

ON SAMPLING-BIORTHOGONAL TIME-DOMAIN SCHEME BASED ON DAUBECHIES COMPACTLY SUPPORTED WAVELETS

2004-04-15

PIER

Vol. 47, 193-212, 2004

doi:10.2528/PIER03121002

download: 185

Numerical Dispersion and Impedance Analysis for 3D Perfectly Matched Layers Used for Truncation of the FDTD Computations

Weiliang Yuan and Er Ping Li

The 3D Berenger's and uniaxial perfectly matched layers used for the truncation of the FDTD computations are theoretically investigated respectively in the discrete space, including numerical dispersion and impedance characteristics. Numerical dispersion for both PMLs is different from that of the FDTD equations in the normal medium due to the introduction of loss. The impedance in 3D homogeneous Berenger's PML medium is the same as that in the truncated normal medium even in the discrete space, however, the impedance in 3D homogenous UPML medium is different, but the discrepancy smoothly changes as the loss in the UPML medium slowly change. Those insights acquired can help to understand why both 3D PMLs can absorb the outgoing wave with arbitrary incidence, polarization, and frequency, but with different efficiency.

NUMERICAL DISPERSION AND IMPEDANCE ANALYSIS FOR 3D PERFECTLY MATCHED LAYERS USED FOR TRUNCATION OF THE FDTD COMPUTATIONS

2004-04-15

PIER

Vol. 47, 135-191, 2004

doi:10.2528/PIER03111702

download: 475

Theoretical Aspects of Wave Propagation in Random Media Based on Quanty and Statistical Field Theory

Nathan Blaunstein

In this work, we summarize the existing theoretical methods based on statistical and quanty theory and give some non-standard mathematical approaches based on such theories to explain the principal scalar and vector electrodynamic problems for future applications to acoustic, radio and optical wave propagation in homogeneous, isotropic, anisotropic and inhomogeneous media. We show of how the statistical description of wave equations can be evaluated based on quantum field theory with presentation of Feynman's diagrams by a limited-to-zero finite set of expanded Green functions according to perturbation theory for single, double, triple, etc, scattering phenomenon. It is shown that at very short wavelengths, the Green's function is damped over a few wavelengths if the refractive index fluctuations in the medium are strong; at long wavelengths the effective phase velocity of electromagnetic waves may be increased. It is shown, that the coupling between different wave modes and the energy transfer between different wave modes, may be important, even for week random fluctuations of parameters of the medium, but it takes a very long time.

2004-04-15

PIER

Vol. 47, 123-133, 2004

doi:10.2528/PIER03111701

download: 185

Malvar Wavelet Based Pocklington Equation Solutions to Thin-Wire Antennas and Scatterers

Youri Tretiakov and George Pan

Malvar wavelets are often referred to as smooth local cosine (SLC) functions. In this paper the SLC functions are employed as the basis and testing functions in the Galerkin-based Method of Moments (MoM) for the Pocklington equation of thin-wire antennas and scatterers. The SLC system has rapid convergence and is particularly suitable to handle electrically large scatterers, where the integral kernel behaves in a highly oscillatory manner. Numerical examples demonstrate the scattering ofelectromagnetic waves from a thin-wire scatterer as well as wave radiation from the gull-shaped antenna. A comparison ofthe new approach versus the traditional MoM is provided.

MALVAR WAVELET BASED POCKLINGTON EQUATION SOLUTIONS TO THIN-WIRE ANTENNAS AND SCATTERERS

2004-04-15

PIER

Vol. 47, 111-121, 2004

doi:10.2528/PIER03102501

download: 285

Analysis of Circularly Polarized Dielectric Resonator Antenna Excited by a Spiral Slot

Z. H. Qian , Kwok Leung and Ru-Shan Chen

The hemispherical dielectric resonator antenna (DRA) excited by a single-arm spiral slot is studied theoretically in this paper. The Green's function technique is employed to formulate an integral equation for the spiral slot current. The moment method with piecewise sinusoidal (PWS) basis and testing functions is used to convert the integral equation into a matrix equation by using a deltagap exciting source. The input impedance, return loss, axial ratio and radiation pattern are calculated. Numerical results demonstrate that the analysis is efficient.

ANALYSIS OF CIRCULARLY POLARIZED DIELECTRIC RESONATOR ANTENNA EXCITED BY A SPIRAL SLOT

2004-04-15

PIER

Vol. 47, 75-85, 2004

doi:10.2528/PIER03100901

download: 199

Compact and Broadband Microstrip Patch Antenna for the 3G IMT-2000 Handsets Applying Styrofoam and Shorting-Posts

Ya Wang and C. Lee

The objective of the paper is to develop a compact and broadband microstrip patch antenna for the IMT-2000 mobile handset application. By parasitically coupling two shorted semi-disc patches with a single shorting-post each and employing Styrofoam substrate with low dielectric constant, an overall impedance bandwidth of 17.8% has been achieved to cover the frequency spectra of 1.862-2.225 GHz. The overall dimension of this proposed antenna is 44.4mm(length) Ã— 37.8mm(width) Ã— 7mm (thickness), and it would be suitable for the IMT-2000 mobile handset application. The typical antenna characteristics are presented and analysed theoretically and experimentally.

COMPACT AND BROADBAND MICROSTRIP PATCH ANTENNA FOR THE 3G IMT-2000 HANDSETS APPLYING STYROFOAM AND SHORTING-POSTS

2004-04-15

PIER

Vol. 47, 61-73, 2004

doi:10.2528/PIER03100101

download: 438

Coupling Cross Section and Shielding Effectiveness Measurements on a Coaxial Cable by Both Mode-Tuned Reverberation Chamber and Gtem Cell Methodologies

Ya Wang , Wee Jin Koh and C. Lee

The field-to-cable coupling cross section is proposed to evaluate the coupling performance of a single-braided coaxial cable. In addition, a new definition for the coax shielding effectiveness is suggested. Both the coupling cross section and the shielding effectiveness of a 1.25 m-length RG 58 C/U 50Î© coax are measured byemplo ying both the mode-tuned reverberation chamber and GTEM cell methodologies. The detailed measurement set-ups and results are presented. The mode-tuned reverberation chamber methodologyis proven to be beneficial for assessing the cable shielding and coupling characteristics over a wide frequencyrange.

COUPLING CROSS SECTION AND SHIELDING EFFECTIVENESS MEASUREMENTS ON A COAXIAL CABLE BY BOTH MODE-TUNED REVERBERATION CHAMBER AND GTEM CELL METHODOLOGIES

2004-04-15

PIER

Vol. 47, 49-60, 2004

doi:10.2528/PIER03092501

download: 202

Application of the Improved Finite Element-Fast Multipole Method on Large Scattering Problems

Xing-Chang Wei , Er Ping Li and Yao Jiang Zhang

The finite element hybridized with the boundary integral method is a powerful technique to solve the scattering problem, especially when the fast multipole method is employed to accelerate the matrix-vector multiplication in the boundary integral method. In this paper, the multifrontal method is used to calculate the triangular factorization of the ill conditioned finite element matrix in this hybrid method. This improves the spectral property of the whole matrix and makes the hybrid method converge very fast. Through some numerical examples including the scattering from a real-life aircraft with an engine, the accuracy and efficiency of this improved hybrid method are demonstrated.

APPLICATION OF THE IMPROVED FINITE ELEMENT-FAST MULTIPOLE METHOD ON LARGE SCATTERING PROBLEMS

2004-04-15

PIER

Vol. 47, 27-47, 2004

doi:10.2528/PIER03081401

download: 165

3-Dimensional Implementation of the Field Iterative Method for Cavity Modeling

Chao-Fu Wang , Yuan Xu and Yeow-Beng Gan

The analysis of electromagnetic scattering from cavity structure is very important to many practical applications. The field iterative method (FIM) is one of the promising methods to deal with the cavity problem. In this paper, 3-dimensional (3D) FIM has been implemented using Rao-Wilton-Glisson (RWG) basis function and an accurate equivalent model of the cavity. Two testing procedures, a newly developed point matching and conventional Galerkin's methods, have been discussed for better and simpler implementation of the 3D FIM. Numerical results show that the accuracy of the 3D implementation of FIM using the newly developed point matching method is the same as that of the conventional Galerkin's method. The numerical results also show that the simpler implementation of 3D FIM using the point matching method converges very fast for all the tested cases.

3-DIMENSIONAL IMPLEMENTATION OF THE FIELD ITERATIVE METHOD FOR CAVITY MODELING

2004-04-15

PIER

Vol. 47, 1-25, 2004

doi:10.2528/PIER03080102

download: 322

Electromagnetic Field Solution in Conformal Structures: Theoretical and Numerical Analysis

Filiberto Bilotti , Andrea Alu and Lucio Vegni

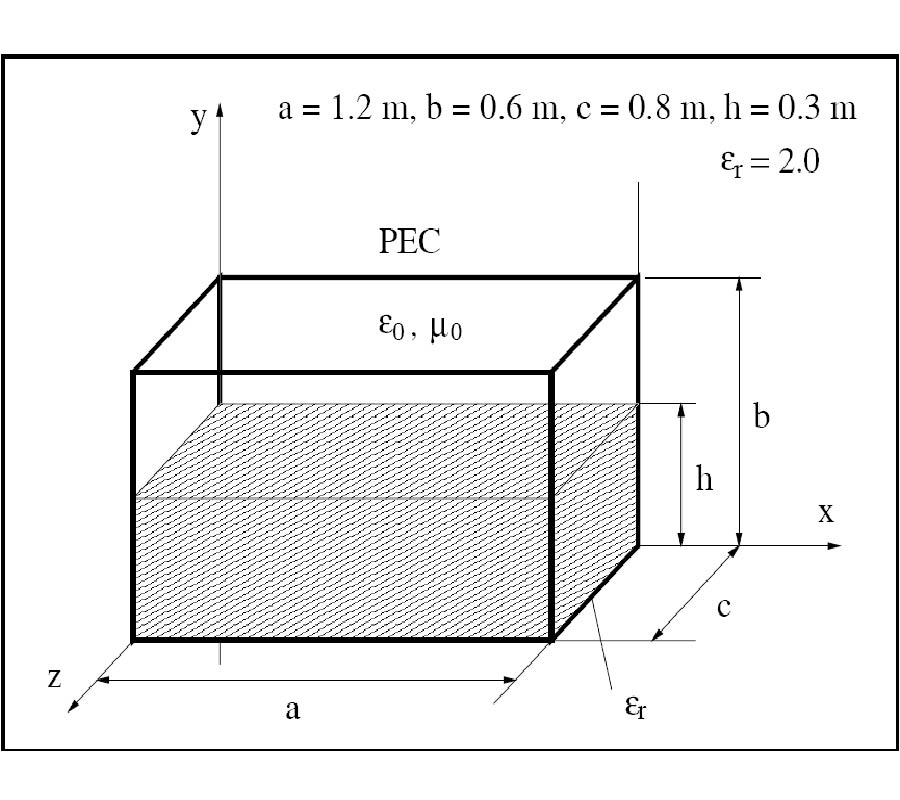
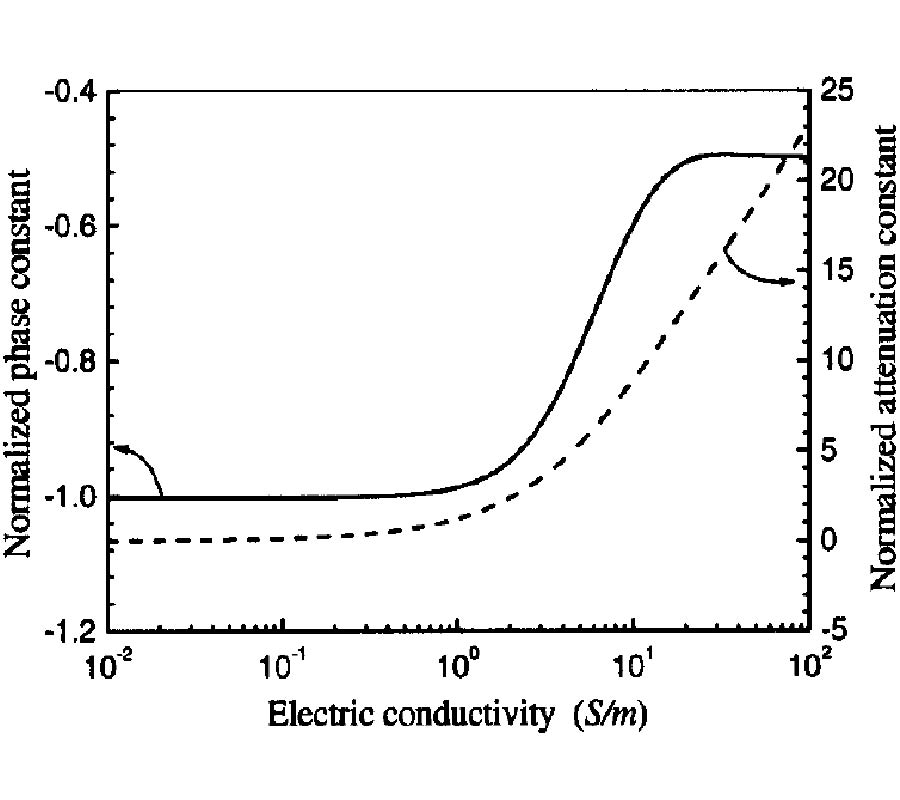
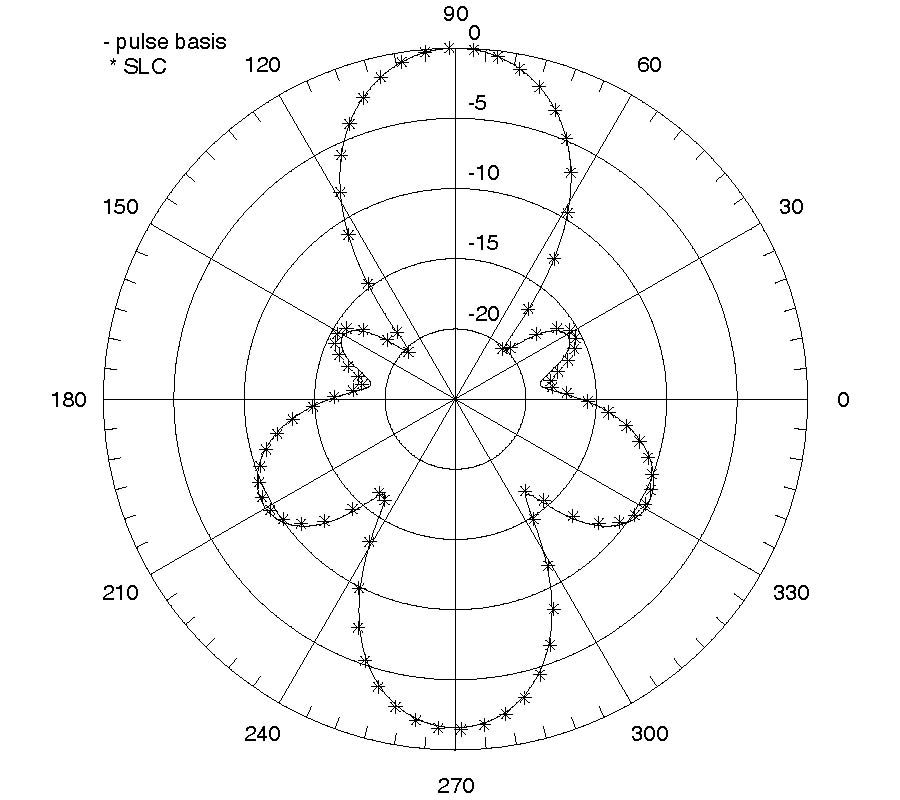
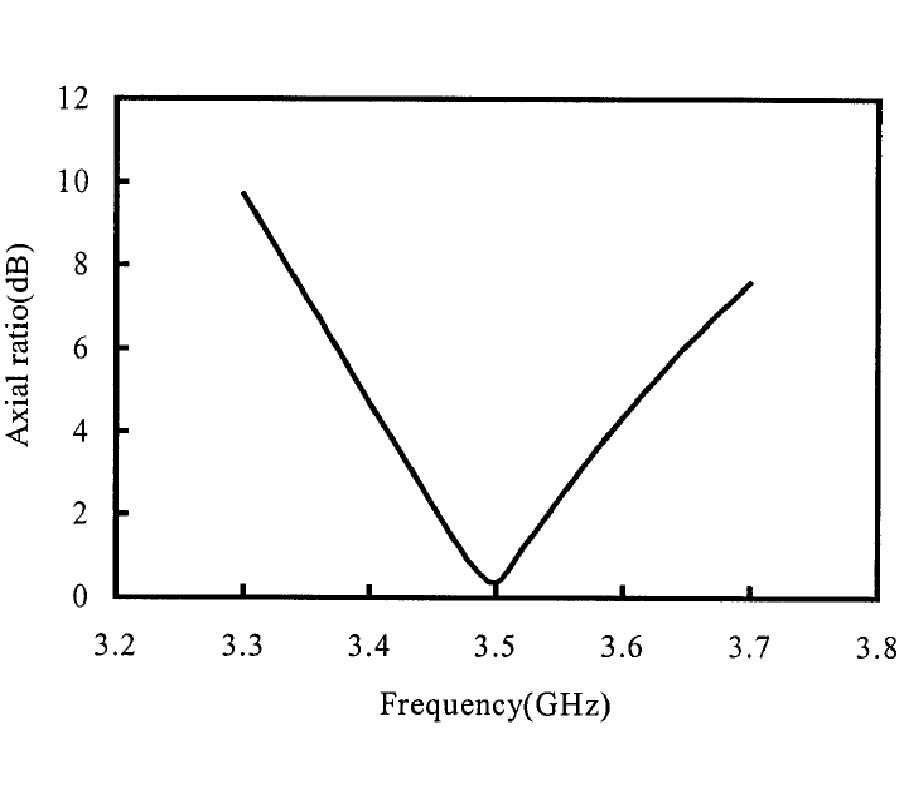
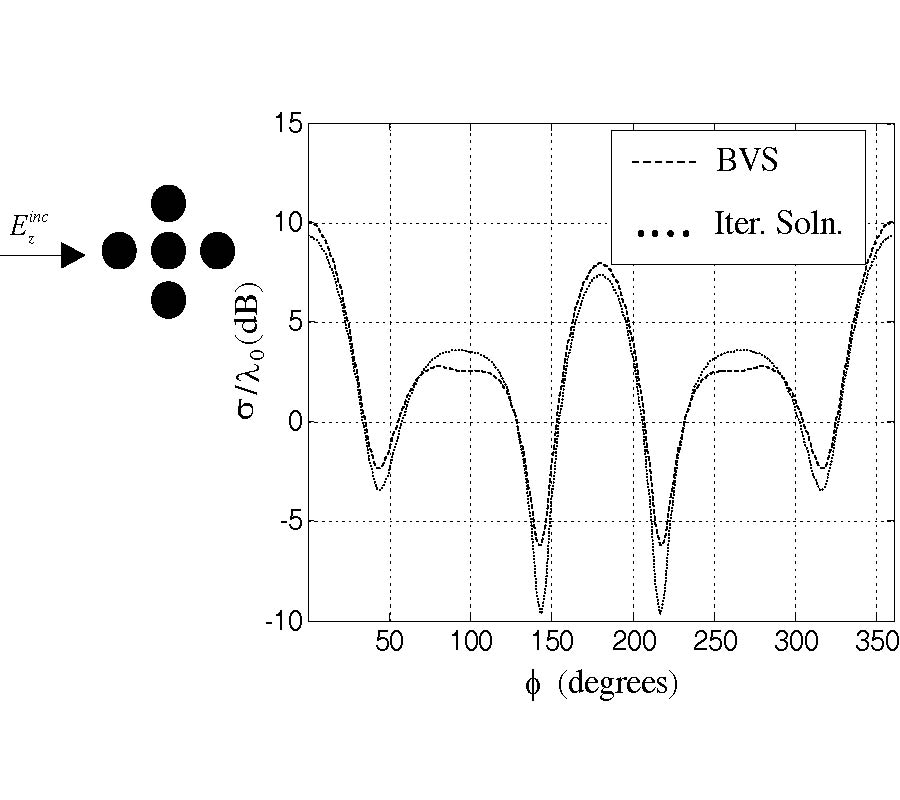
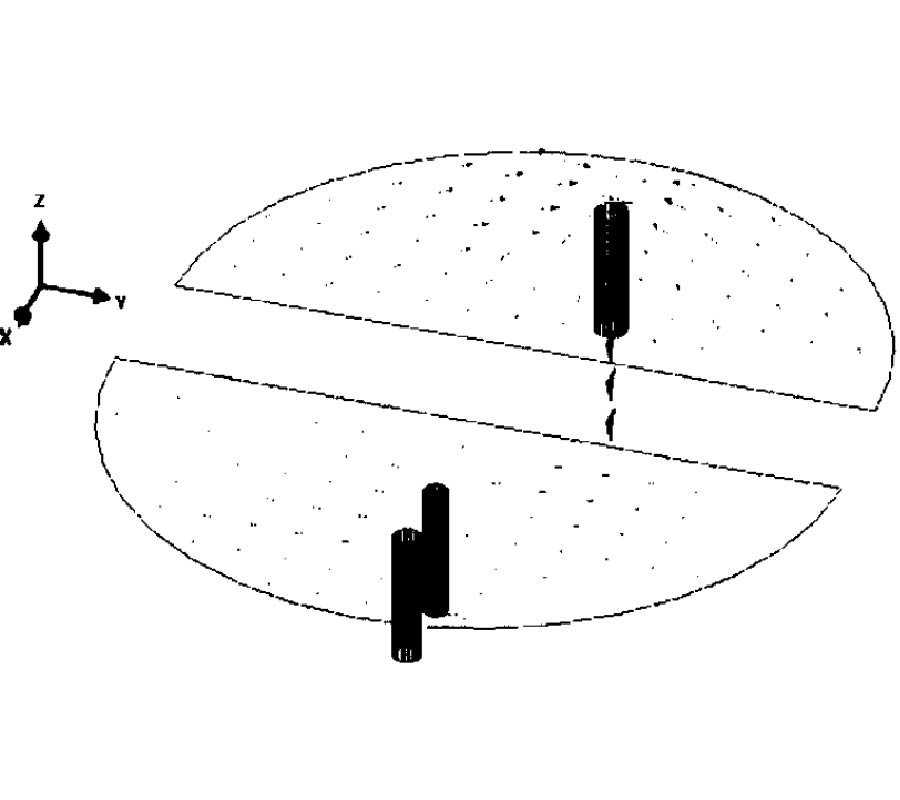
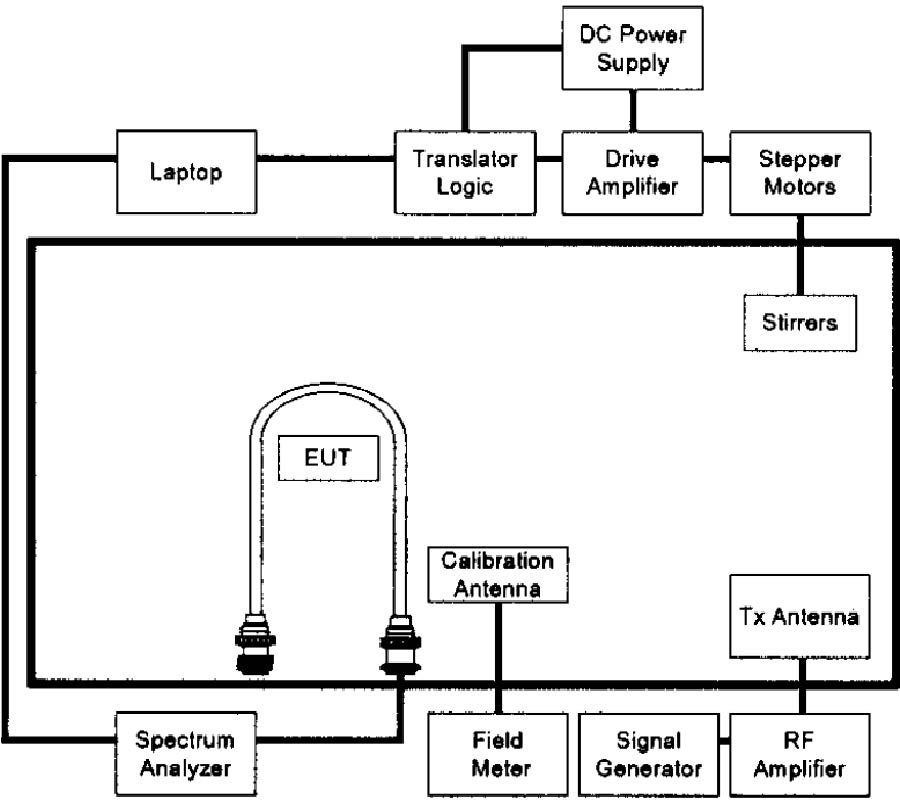
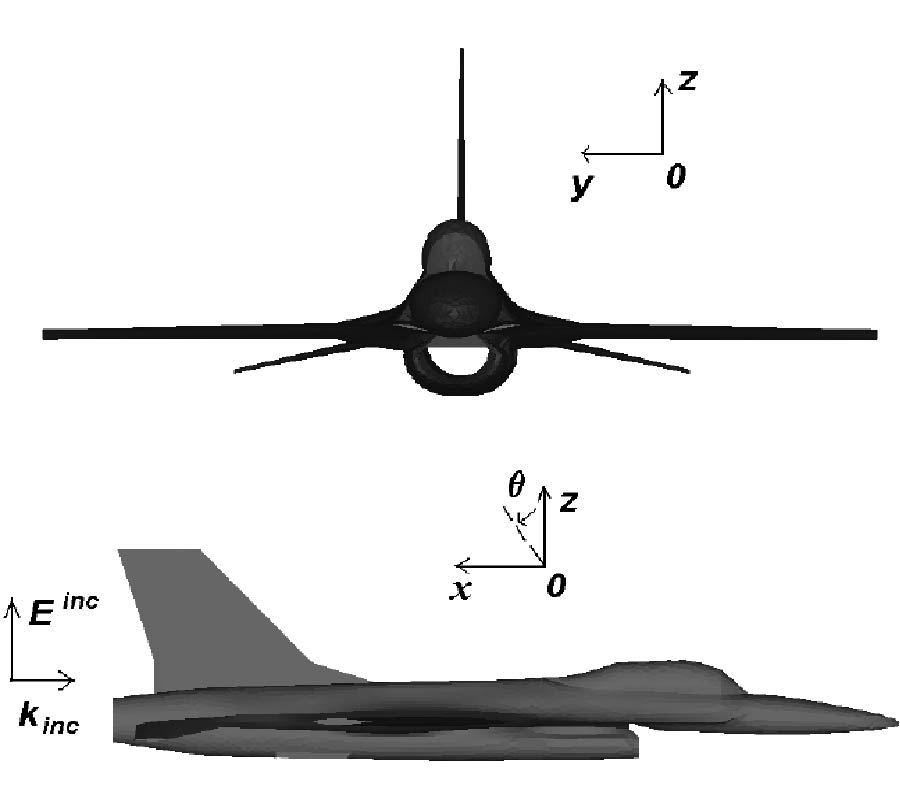
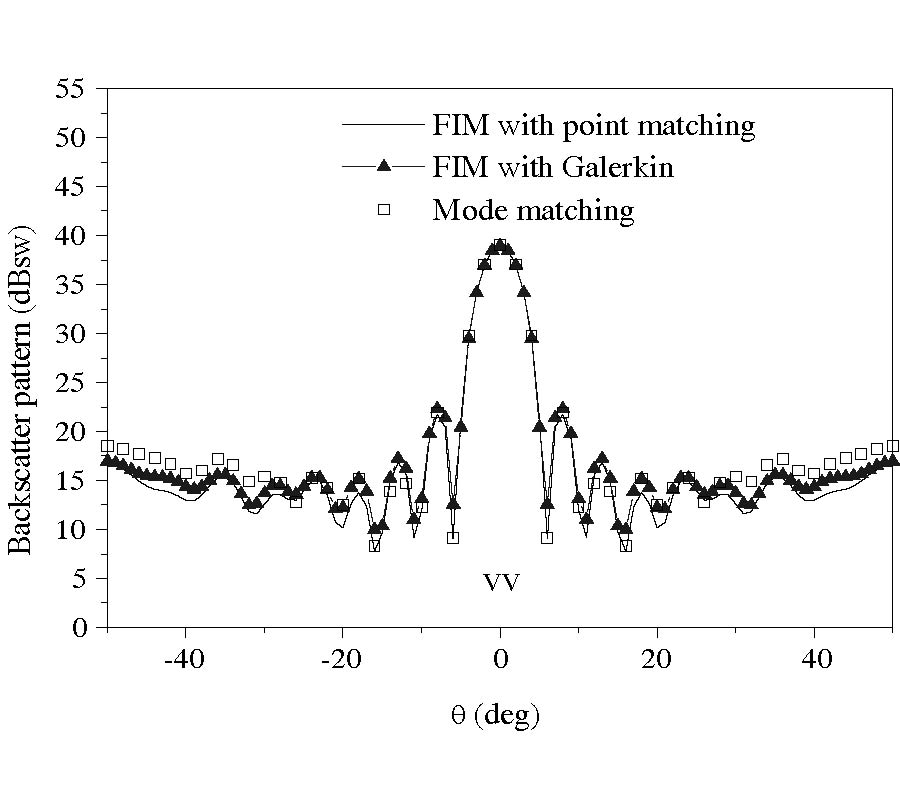
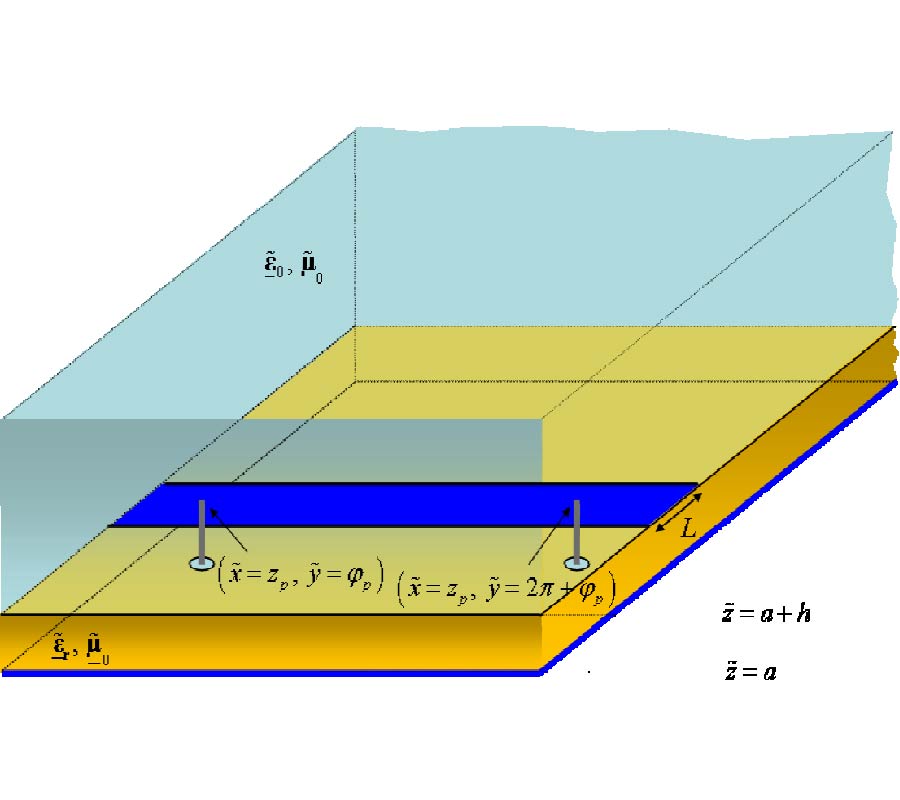
A full-wave evaluation of the electromagnetic field in conformal structures with linear loading materials is presented in this paper. The analysis is performed considering at first conformal components with conventional isotropic and homogeneous media in the generalized orthogonal curvilinear reference system. In this first case, a summary of the possible analytical solutions of the vector wave equation obtainable through various factorization techniques is given. Then, the attention is focused on conformal structures involving non-conventional media (anisotropic, chiral, bianisotropic) and in this case the field solution is demanded to a new generalization of the transmission line approach. As an aside, exploiting a contravariant field formulation, which allows writing Maxwell's equations in the generalized reference system as in the Cartesian one, a useful relationship between the local curvature of the geometry and a suitable inhomogeneity of a related planar structure is presented. Finally, some results, obtained simulating the behavior of patch radiators mounted on curved bodies through the combined application of an extended Method of Line (MoL) numerical algorithm and the theoretical approach here derived, are presented.